
This value is the quantity of imperfections in this scale.

Cohemitonia describes how many such cohemitones exist.Īn imperfection is a tone which does not have a perfect fifth above it in the scale. Hemitonia describes how many such hemitones exist.Ī cohemitone is an instance of two adjacent hemitones. If a scale is chiral, then it has an enantiomorph.Ī hemitone is two tones separated by a semitone interval. Notably an axis of reflection can occur directly on a tone or half way between two tones.Ī palindromic scale has the same pattern of intervals both ascending and descending.Ī chiral scale can not be transformed into its inverse by rotation. It also implies that the scale has Ridge Tones. If a scale has an axis of reflective symmetry, then it can transform into itself by inversion. If there are any rotational symmetries, these are the intervals of periodicity. Some scales have rotational symmetry, sometimes known as "limited transposition".
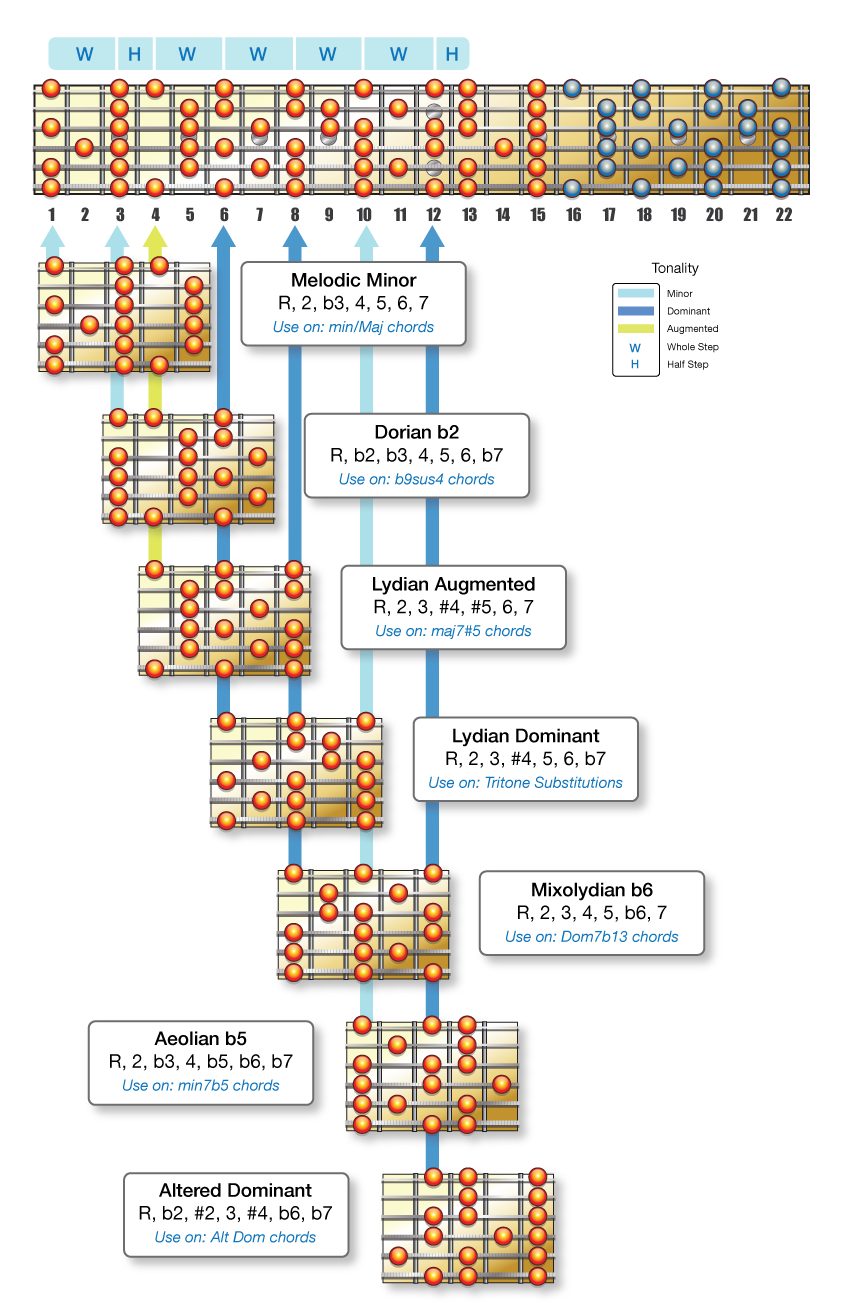
#Melodic minor scale code
The tones in this scale, expressed as numbers from 0 to 11Ī code assigned by theorist Allen Forte, for this pitch class set and all of its transpositional (rotation) and inversional (reflection) transformations. For example, in the G melodic minor scale we have both a B flat and an F sharp.Cardinality is the count of how many pitches are in the scale. Unlike the major and natural minor scales, it is possible to have sharps and flats in the same melodic minor scale. Also, when you get back to scale degree 1 at the end of the scale, make sure that it is also G. For example, if your first pitch is a G, and your 8th scale degree is G sharp, an error has been made.
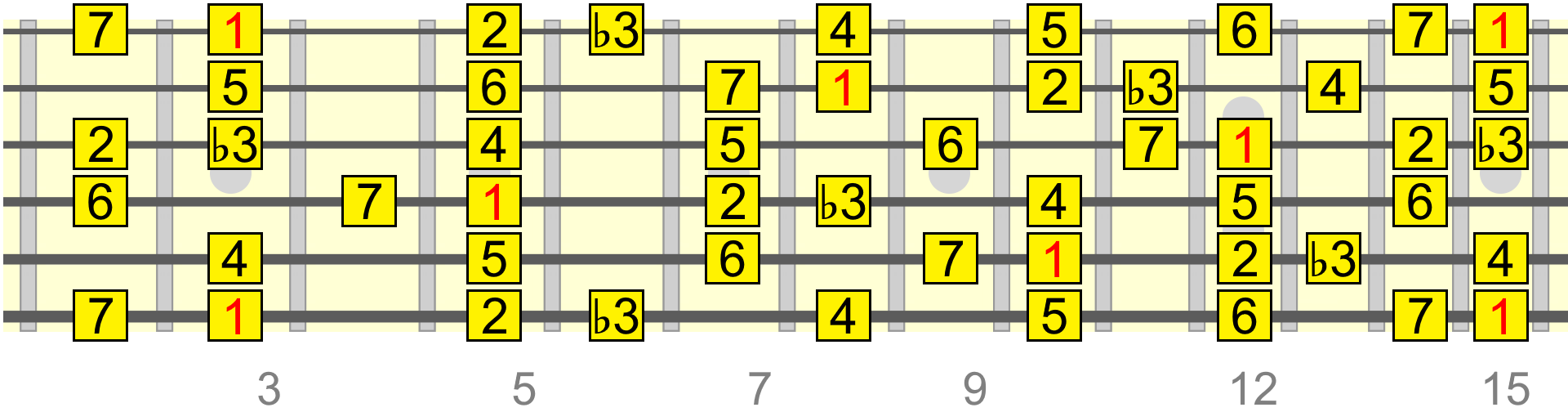
The first and the 8th scale degree of the melodic minor scale should be exactly the same pitch an octave apart. It is good practice to always include accidentals for scale degrees 6 and 7 for the descending part of the melodic minor scale. You must write the natural sign in front of the F in the descending section of the G melodic minor scale otherwise it will be interpreted as an F sharp because that was written for the ascending part of the scale. By going through each whole step and half step we can complete the melodic minor scale. Check every whole step and half step in the scale and write in the appropriate accidentals. Also, the last note should be exactly the same as your first note, so in this case your last note should be G.Ĥ. Make sure that scale degree 8 is exactly one octave above the first note of the scale. Do not skip any pitches and do not repeat any pitches. Start on the note G and write each successive note for each scale degree. Write in the pitches for the diatonic scale. (1 W 2 H 3 W 4 W 5 W 6 W 7 H 8 and then 8 W 7 W 6 H 5 W 4 W 3 H 2 W 1).ģ. Write the pattern of whole steps and half steps as they occur between each scale degree:

Write all of the scale degrees under the staff, both ascending and descending.Ģ. Here is a simple step-by-step process to create melodic minor scales accurately, with the G melodic minor scale as an example.ġ. No letter names will be repeated or skipped. Like the natural minor scale, the melodic minor is a diatonic scale. When the scale is ascending, the pattern of whole steps and half steps is as follows:ĭescending, the melodic minor scale is the same as a descending natural minor scale: The melodic minor scale is unlike the natural minor scale because the pitches are different depending on whether the scale is ascending or descending.


 0 kommentar(er)
0 kommentar(er)
